 |
Implications of Heat Transport in Solids Depending on Length-Scale |
Anne M. Hofmeister
Department of Earth and Planetary Science, Washington University, St Louis, MO 63130, USA;
hofmeist@wustl.edu
This webpage is a summary of: Hofmeister, A.M. (2021) Dependence of Heat Transport in Solids on Length-scale, Pressure, and Temperature: Implications for Mechanisms and Thermodynamics. Materials 14, Paper 449. (Open access at https://www.mdpi.com/1996-1944/14/2/449)
Overview
The alleged existence of plumes requires heat conduction in the mantle to be inefficient. Heat transport and its governing material properties have been misunderstood because these are based on measurements of thermal conductivity (κ) involving large systematic errors with opposing signs. The paper [1] described here, and earlier efforts [2], provide accurate measurements of thermal diffusivity (D) as a function of temperature (T) and the sample length (L) across which heat diffuses plus a theory for diffusion of radiation. This is further tested against available, reliable low-pressure (P) data on ∂(ln κ)/∂P. Implications for the mantle are discussed below.
Method
Laser Flash Analysis (LFA) was used to construct a large database for D on ~200 non-metallic crystals, ~100 silicate glasses, and ~30 metals above ~298°K. Errors associated with LFA are less than half those of other methods [3] since physical contacts and spurious boundary-to-boundary radiative transfer are avoided.
Results
Length-scale. Metals, alloys, semi-conductors (Figure 1) plus glassy and crystalline insulators adhere to:
D(L,298K) = D∞[1-exp(-bL)] (1)
Similar formulae describe higher temperatures. At L = 0, D = 0 because diffusion of heat requires a medium. The parameter D∞ represents thermal diffusivity at 298 K for a long sample whereas parameter b represents attenuation of the heat transmitted. Attenuation losses as light traverses a sample are defined by the absorption coefficient:
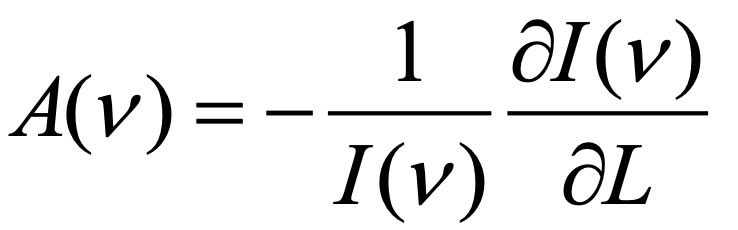 (2) (2)
As is well-known, light heats matter, depending on the frequency, v.
Furthermore, one formula relates b to D∞ for diverse solids at a given temperature. These findings show that the same mechanism of heat conduction operates regardless of bonding type. Regarding electrons in metals, fast experiments on long lengths show that these carry little heat and only transiently [4].
Grain-size has an additional effect which is tied to the porosity and pore fillings [5]. This is not important in the mantle because air and water fillings are removed during compression due to their buoyancy and high mass diffusivity.
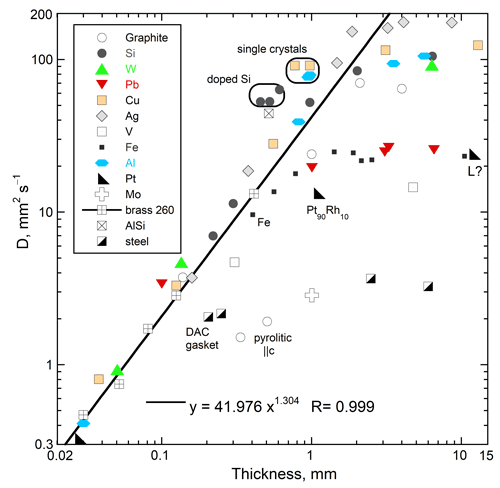
Figure 1. Log-log dependence of D at 298 K on thickness for various elements and alloys. The power law fit is to brass and only for L < 0.5 mm. The steels are non-magnetic. Reproduction of Figure 8b from [1], which has a creative commons license.
Pressure. Previous piston-cylinder experiments describe macroscopic (>1 mm) samples and initial gradients (P<2 GPa). Logarithmic derivatives (Figure 2) reduce the effect of systematic errors.
Diffusion of radiation under optically thick conditions at all frequencies in one Cartesian direction (parallel rays) is described by:
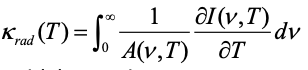 (3) (3)
Combining (2) and (3) provides:
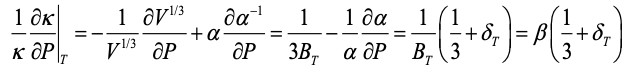 (4) (4)
where B is bulk modulus. Previous formulae, based on dimensional analyses, lack the thermal expansivity (α) term. This term stems from conduction involving a thermal gradient, rather than constant T. Equation (4) corrects a sign error in a middle term in Eq. (42) of [1]. Reliable data on all types of solids adhere to Eq. (4) within the uncertainty of the measurements.
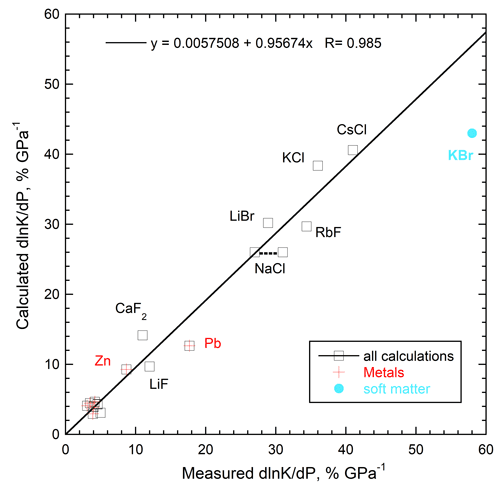
Figure 2. Calculations using Eq. (4) compared to measured heat transport data at pressure from Table 3 of [1]. KBr exemplifies the soft, hydroscopic alkali halides (bulk modulus < 16 GPa). Data sources include [6,7,8]. After figure 15 in [1].
Temperature. Equation (3), with Planck’s idealization for I(v) and simple approximations for A(v), fits the thermal conductivity of diverse solids [2]. At low T, infrared absorption is relevant. Using a boxcar function with a cutoff frequency reasonably describes the peak in κ for corundum (Figure 3). The other fitting parameter is maximum A, which controls the peak in κ(T). Metals are better fit with a triangle function for A, which likewise is defined by a cutoff frequency and a maximum. However, metals strongly absorb into the near-IR which requires evaluating near-IR absorption. Existence of higher frequency absorption (i.e. a second boxcar) provides a second, higher T peak in κ, as in steel (Figure 3).
Due to A(v) varying widely among solids, κ(T) and D(T) also vary. Even so, for larger than mm sizes, the 3-parameter formula for T > 298 K discovered for insulators [9]:
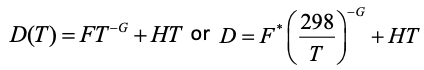 (5) (5)
also describes semi-conductors and metals [1]. For several metals and alloys, the HT term dominates even at 298 K [1,4].
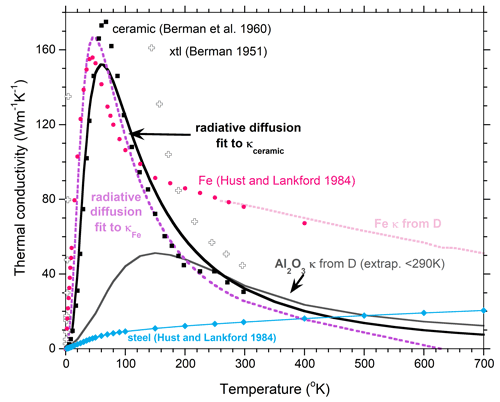
Figure 3. Examples of cryogenic thermal conductivity, which can be fit with a few parameters which describe how the material absorbs light. Results from Figures in [1] and [2] are combined. Cryogenic data from [10,11,12].
Summary. Our results show that diffusion of radiation is the mechanism for heat conduction in solids. This finding is consistent with Fourier’s equations, which assumes that heat is a fluid flowing through matter. Importantly, the photon is real, unlike phonons which are pseudo-particles. Moreover, photons readily leave a body during heat transfer, unlike phonons or electrons, which is required to explain ever-present thermal emissions.
Problematic high-P, high-T diamond anvil cell (DAC) experiments
Use of ultrathin samples in DAC studies should provide miniscule κ-values (Eq. 1). However, length-scale effects went unnoticed due to benchmarking DAC extractions against κ for ~mm sized samples at 1 atm. Thermo-reflectance results rest on benchmarking because the distance over which heat diffuses is unknown (see [2,3]). Additional problems accompany laser heating DAC studies. The imposed thermal gradient in some experiments on Fe by [13] had the opposite sign than that assumed in their models, yet similar values for κ were obtained regardless of whether dT/dL permitted rearwards conduction.
Implications for the Earth
Our results show that heat is light, which at low temperatures lies in the infrared region. As temperatures climb, higher frequencies of light participate in conduction. With mantle candidate materials transmitting about 1000x more light in the visible than in the infrared for Fe/Mg near 0.1, and the flux from a hot body going roughly as T4, radiative conduction is efficient in the mantle, and increasingly so with depth. Compression further enhances conduction (Eq. 4).
Recent conductive cooling models of Earth’s interior were based on transport properties measured at modest T [14]. The higher frequency augmentation of κ was not addressed, yet temperatures ascertained were consistent with a solid mantle. From the findings in [1], the deep Earth is a much better conductor of heat than previously envisioned. As it is accepted that Earth’s heat sources are inadequate to cause mantle convection [15], we have recently proposed that gravitational torques cause motions of plates near Earth’s surface [16].
References
[1] Hofmeister, A.M. (2021) Dependence of Heat Transport in Solids on Length-scale, Pressure, and Temperature: Implications for Mechanisms and Thermodynamics. Materials, 14, Paper 449.
[2] Hofmeister, A.M. (2019). Measurements, Mechanisms, and Models of Heat Transport; Elsevier: Amsterdam, The Netherlands.
[3] Zhao, D.; Qian. X.; Gu, X.; Jajja, S.A.; Yang, R. (2016) Measurement techniques for thermal conductivity and interfacial thermal conductance of bulk and thin film materials. J. Electron. Packag., 138, 040802.
[4] Criss, E.M.; Hofmeister, A.M. (2017) Isolating lattice from electronic contributions in thermal transport measurements of metals and alloys and a new model. Int. J. Mod. Phys. B, 31, 1750205
[5] Branlund J.M. and Hofmeister A.M. (2008) Factors affecting heat transfer in SiO2 solids. American Mineralogist 93, 1620-1629
[6] Andersson, S.; Bäckström, G. (1986) Techniques for determining thermal conductivity and heat capacity under hydrostatic pressure. Rev. Sci. Instrum., 57, 1633–1639.
[7] Andersson, P. (1985) Thermal conductivity under pressure and through phase transitions in solid alkali halides. I. Experimental results for KCl, KBr, KI, RbCl, RbBr and RbI. J. Phys. C Solid State Phys., 18, 3943–3955.
[8] Sundqvist, B. (1982) Transport properties of iron and nickel under pressure. In High Pressure in Research and Industry, Proceedings of the 8th AIRAPT Conference and 19th EHPRG Conference, University of Uppsala, Sweden, 17–22 August 1981; Backman, C.M., Johannison, T., Tegnér, T., Eds.; Arkitektkopia: Stockholm, Sweden, 432–433
[9] Hofmeister, A.M.; Dong, J.J.; Branlund, J.M. (2014) Thermal diffusivity of electrical insulators at high temperatures: Evidence for diffusion of phonon-polaritons at infrared frequencies augmenting phonon heat conduction. J. Appl. Phys., 115, 163517.
[10] Hust, J.G.; Lankford, A.B. Update of thermal conductivity and electrical resistivity of electrolytic iron, tungsten, and stainless steel. Natl. Bur. Stand. Spec. Pub., 1984, 260, 90.
[11] Berman R.; (1951) The thermal conductivities of some dielectric solids at low temperatures. Proc. Royal Soc. Lond. A, 208, 90-108.
[12] Berman, R., Foster, E.L., Schneidmesser, B., Tirmizi, S.M.A.; (1960) Effects of irradiation on the thermal conductivity of synthetic sapphire. J. Appl. Phys., 31, 2156-2159.
[13] Konôpková, Z.; McWilliams, R.S.; Gómez-Pérez, N.; Goncharov. A.F. Direct measurement of thermal conductivity in solid iron at planetary core conditions. Nature, 534, 99–101.
[14] Criss, R.E. and Hofmeister, A.M. (2016) Conductive cooling of spherical bodies with emphasis on the Earth. Terra Nova, 28, 101-109.
[15] Bercovici, D.; (2015) Mantle Dynamics: An Introduction and Overview. In: Schubert, G., ed., Treatise on Geophysics, vol. 7: 1–22 (Elsevier, Amsterdam, Netherlands).
[16] Hofmeister, A.M.; Criss, R.E.; Criss, E.M. (2021) Link of Planetary Energetics to Moon Size, Orbit, and Planet Spin: A New Mechanism for Plate Tectonics. In: In the Footsteps of Warren B. Hamilton: New Ideas in Earth Science (Geological Society of America Special Paper 553); Foulger, G.F.; Jurdy, D.M., Stein, C.A.; Hamilton, L.C.; Howard, K.; Stein, S. (Eds.) Geological Society of America: Boulder, CO, USA, 2021; in press. Also see: https://doi.org/10.1130/2021.2553(18).
last updated 29th May, 2021 |
